| Ekstrapolacja
|
| Wyznaczanie wartości funkcji f(x) na zewnątrz
przedziału, w którym funkcja ta jest znana (mat.). |
| |
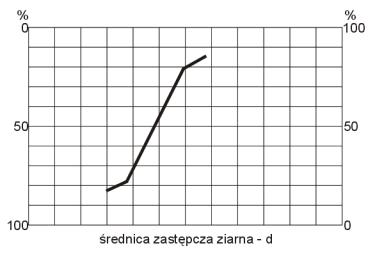
| Krzywa bez ekstrapolacji |
Przypadek "zawieszonej krzywej" wystąpi na przykład, gdy na pierwszym
sicie zanotowaliśmy masę (dolna część wykresu) natomiast
na ostatnim sicie nie uzyskaliśmy 100% masy (górna część
wykresu). Taka sytuacja przysparza często problemów
w znalezieniu skrajnych wartości centyli i oznaczenia
skrajnych wartości średnic oraz wykonaniu dalszych obliczeń.
W
celu rozwiązania tych trudności stosuje się ekstrapolacje. |
 |
| |
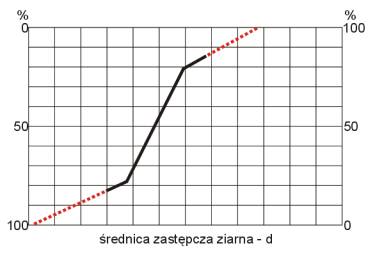
| Przedłużanie (ekstrapolacja) Folka i Warda |
Polega ona na konsekwentnym przedłużaniu ostatniego segmentu krzywej kumulacyjnej,
doprowadzając: na siatce prawdopodobieństwa do wartości
1% (99%), na siatce arytmetycznej do wartości 0% (100%).
Metoda wprowadzona przez Folka i Warda (1957).
|
 |
| |
| Przesunięcie (ekstrapolacja)
o 3 phi |
| Wykres osiąga wartość graniczną po trzech pełnych jednostkach phi
. |
| |
| Aproksymacja
|
Zastąpienie jednych wielkości matematycznych (funkcji, liczb) przez inne (przybliżone)
- prostrze, łatwiejsze do badania i stosowania.
Wygładzenie
przebiegu krzywej.
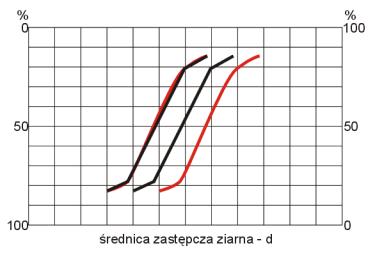
Przykład:
krzywa
łącząca poszczególne sita liniami prostymi (kolor czarny)
krzywa
aproksymowana (kolor czerwony)
nałożenie obydwóch
krzywych odzwierciedla różnice w przebiegu linii
.
|
 |
| |
| Graficzne
metody przedstawienia wyników analiz |
Trójkąt
Fereta
(wykres trójkątny) - graficzna metoda odwzorowywania
składu osadu/gruntu. Jednym punktem w układzie współrzędnych
trójkątnych przedstawia się trzy elementy składowe -
najczęściej % udział frakcji podstawowych. Stosowana
jest powszechnie w wielu dziedzinach: sedymentologii,
hydrogeologii. gleboznawstwie itd.
|
|
Krzywa
kumulacyjna
(dystrybuanta) - graficzna metoda przedstawiająca
rozkład uziarnienia. Krzywa skumulowanej wartości procentowej
przedstawiona w kartezjańskim układzie prostokątnych
osi współrzędnych x, y. Najczęściej na osi odciętych
zaznacza się średnice, na osi rzędnych - procentową
zawartość materiału w osadzie.
|
|
Histogram
(wykres kolumnowy) - graficzny sposób przedstawienia
rozkładu elementów zbioru na poszczególne kategorie,
czyli przedziały klasowe.
|
|
Krzywa
częstości
|
Krzywa częstości rozkładu wielkości ziaren (krzywa
częstości uziarnienia) - jest obrazem graficznym rozkładu
zmiennej typu ciągłego. W praktyce krzywą częstości
uziarnienia uzyskuje się na drodze pośredniej, jako
wynik różniczkowania krzywej kumulacyjnej.
|
|
| Wzajemne
relacje podstawowych wskaźników uziarnienia |
|
(zestawy par wskaźników, diagramy rozproszenia)
- charakterystyka litodynamiczna pozwalająca odtworzyć
warunki dynamiczne środowisk sedymentacyjnych. Można
zestawiać różnego rodzaju wskaźniki, ale najczęściej
spotykane to średnia średnica do wysortowania, spłaszczenia,
skośności.
|
|
| Diagram
C/M R. Passegi
|
Diagram rekonstrukcji dynamiki środowiska sedymentacyjnego.
Zbudowany na podstawie układu dwu osi współrzędnych.
Na osi rzędnych zaznacza się pierwszy centyl rozkładu
uziarnienia, na osi odciętych zaznacza się wartość mediany
rozkładu uziarnienia. |
|
|
Parametry
rozkładu uzirnienia
|
Średnia
średnica |
przeciętna wielkość ziaren, GSS, Mz |
W sposób ogólny informuje o przeciętnej średnicy ziaren w danym rozkładzie.
Niekiedy jest określana również mediana, czyli średnica ziaren, która wraz
z większymi stanowi 50% masy osadu, lub wartość modalna,
charakteryzująca średnicę ziaren występującą w największej
częstości w rozkładzie jednomodalnym.
Pojęcia: średnia średnica lub przeciętna wielkość ziarna należy rozumieć jako
średnicę zastępczą, bez bliższego sprecyzowania; zależną
od stosowanej metody laboratoryjnej.
|
|
Wysortowanie |
rozproszenie, odchylenie standardowe, dyspersja, GSO, d1 |
Charakteryzuje rozrzut składników w danym rozkładzie uziarnienia informując,
czy osad jest pod względem wielkości ziaren dobrze lub
słabo wysortowany.
|
|
Skośność |
asymetria, GSK, Sk1
|
Wskazuje, czy rozkład uziarnienia ma charakter symetryczny względem wartości
modalnej, czy też ramiona krzywej gęstości mają różne
nachylenie w stronę średnic grubych i drobniejszych.
|
|
Spłaszczenie |
eksces, kurtoza, GSP, KG |
Informuje, w jakim stopniu centralna część rozkładu uziarnienia odbiega od
rozkładu normalnego, czy analizowaniy rozklad jest bardziej
spłaszczony czy też bardziej wysmukły od rozkładu normalnego.
|
|
| Stosowane
wskaźniki i klasyfikacje |
| Klasyfikacje
osadów okruchowo-ilastych na podstawie uziarnienia |
| Podstawowym kryterium klasyfikacji luźnych osadów
okruchowo-ilastych jest wielkość składników tworzących
dany utwór. Przyjmuje się, że rozpad skały litej przebiega
stopniowo od fragmentów blokowo-kamiennych przez głazowe, żwirowe, piaskowe do pyłowych (mułkowych) i iłowych.
Frakcje podane powyżej są traktowane jako główne (podstawowe), ale granice
między nimi przyjmowanne są w sposób odmienny w zależności
od obowiązujących norm i wytycznych w danej dziedzinie.
Czasami można spotkać się z odmiennym nazewnictwem.
|
| Podstawy wyodrębniania frakcji głównych (podstawowych)
(wartości przedziałów frakcji wg R. Racinowski, T. Szczypek 1985) |
|
Frakcja głazowa - powyżej 200 mm.
W polskich osadach występuje ona sporadycznie dlatego też jest traktowana
ogólnie.
|
|
| Frakcja kamienista - 200-40 mm.
Występują tu wielomineralne fragmenty skał będące efektem wietrzenia oraz
niszczenia mechanicznego w trakcie transportu wodnego
lub lodowcowego. W Polsce, w osadach czwartorzędowych,
stanowi domieszkę do 10%.
|
|
| Frakcja żwirowa - 40-2 mm.
Nazywana frakcją przejściową ze względu na jakość składników. Występują tu
okruchy polimineralne i ziarna monomineralne będące
efektem wietrzenia skał litych i rumoszu bądź powstałe
w wyniku mechanicznego rozdrobnienia materiału grubszych
frakcji podczas transportu wodnego, lodowcowego lub
eolocznego.
|
|
| Frakcja piaskowa - 2-0,05 mm.
W polskich osadach składa się na nią materiał monomineralny, a sporadycznie
ziarna wielomineralne. Skrajne przedziały tej frakcji
charakteryzują się podobnymi prędkościami erozyjnymi.
Pod względem hydrogeologicznym frakcja jest wodoprzepuszczalna
i charakteryzuje się występowaniem zjawiska kapilarności.
|
|
| Frakcja pyłowa - 0,05-0,002 mm.
Składniki tej frakcji charakteryzują się osiadaniem w wodzie według prawa
Stockes'a. Podczas transportu poszczególne cząstki pyłu
nie ulegają rozdrabnianiu mechanicznemu. Charakterystycznymi
składnikami frakcji pyłowej polskich osadów kenozoicznych
są: kwarc, łyszczyki, koloidy krzemionki, węglan wapnia
oraz minerały ilaste. Frakcja ta wykazuje znaczną spójność
i higroskopijność oraz odznacza się dużymi wartościami
wzrostu kapilarnego.
|
|
| Frakcja iłowa - poniżej 0,002 mm.
Grupuje się tu większość minerałów ilastych oraz gruntowych minerałów koloidalnych
o różnym stopniu dyspersji. Frakcja ta wykazuje porowatość
subkapilarną, a jednocześnie jest szczególnie podatna
na zjawisko tiksotropii. Składniki frakcji ilastej praktycznie
nie ulegają niszczeniu mechanicznemu, mogą natomiast
podlegać przemianom krystalochemicznym , związanym z
procesem starzenia się koloidów gruntowych. Przemiany
te zachodzą również pod wpływem oddziaływania czynników
chemicznych i biogennych. Skonsolidowany materiał ilasty
z trudem podlega erozji wodnej i niszczeniu eolicznemu,
gdy jednak zostanie wprowadzony do zawiesiny, bardzo
powoli ulega procesowi depozycji i kompakcji.
|
|
| Podstawy wyodrębniania typów osadu |
| Opierając się na relacjach zachodzących między frakcjami podstawowymi przeprowadza
się granulomeryczny podział materiału okruchowo-ilastego
na odrębne typy (rodzaje). Z reguły do celów klasyfikacyjnych
są wykorzystywane trójkąty równoboczne, które w różny
sposób są dzielone na odrębne pola taksonomiczne.
|
|
|
| Wskaźniki
obliczane na podstawie średnich średnic wyrażonych w
skali phi |
| Średnia średnica |
| C. E. Van Orstrand (1925), W. C. Krumbein (1936) - metoda momentów
|
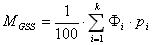 |
gdzie:
|
Øi - punkt środkowy i-tego przedziału
klasowego w jednostkach |
|
pi - częstość i-tego przedziału klasowego
w procentach
k
- liczba przedziałów klasowych |
| R. L. Folk i W. C. Ward (1957)
|
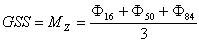 |
| gdzie: |
| Ø16 - średnica ziaren, która wraz z większymi
stanowi 16% masy osadu |
Ø50 - średnica ziaren, która wraz z większymi
stanowi 50% masy osadu |
| Ø84 - średnica ziaren, która wraz z większymi
stanowi 84% masy osadu
|
|
| Wysortowanie |
| C. E. Van Orstrand (1925), W. C. Krumbein (1936) - metoda momentów
|
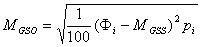 |
| gdzie: |
| Øi - punkt środkowy i-tego przedziału
klasowego w jednostkach |
|
pi - częstość i-tego przedziału klasowego
w procentach
|
| MGSS - moment centralny pierwszego
rzędu
|
| R. L. Folk i W. C. Ward (1957)
|
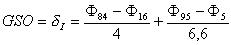 |
| gdzie: |
Ø5 - średnica ziaren, która wraz z większymi
stanowi 5% masy osadu |
Ø16 - średnica ziaren, która wraz z większymi
stanowi 16% masy osadu
|
Ø84 - średnica ziaren, która wraz z większymi
stanowi 84% masy osadu
|
Ø95 - średnica ziaren, która wraz z większymi
stanowi 95% masy osadu
|
gdy: |
GSO < 0,35 - wysortowanie bardzo dobre |
0,35 < GSO < 0,50 - wysortowanie dobre
|
0,50 < GSO < 0,71 - wysortowanie umiarkowanie dobre
|
0,71 < GSO < 1,0 - wysortowanie umiarkowane |
1,00 < GSO < 2,00 - wysortowanie słabe |
2,00 < GSO < 4,00 - wysortowanie bardzo słabe |
| 4,00 < GSO - wysortowanie skrajnie słabe
|
|
| Skośność |
| C. E. Van Orstrand (1925), W. C. Krumbein (1936) - metoda momentów
|
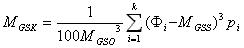 |
gdzie: |
Øi - punkt środkowy i-tego przedziału
klasowego w jednostkach |
pi - częstość i-tego przedziału klasowego
w procentach
k
- liczba przedziałów klasowych |
MGSS - moment centralny pierwszego
rzędu
|
MGSO - moment centralny drugiego rzędu
|
R. L. Folk i W. C. Ward (1957)
|
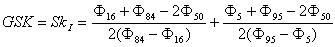
|
gdzie: |
Ø5 - średnica ziaren, która wraz z większymi
stanowi 5% masy osadu |
Ø16 - średnica ziaren, która wraz z większymi
stanowi 16% masy osadu |
Ø50 - średnica ziaren, która wraz z większymi
stanowi 50% masy osadu |
Ø84 - średnica ziaren, która wraz z większymi
stanowi 84% masy osadu |
Ø95 - średnica ziaren, która wraz z większymi
stanowi 95% masy osadu
|
gdy:
|
-1,0 < GSK > -0,3 - bardzo skośny ujemnie |
-0,3 < GSK > -0,1 - skośny ujemnie
|
-0,1 < GSK > +0,1 - w przybliżeniu symetryczny
|
+1,0 < GSK > +0,3 - skośny dodatnio
|
| +0,3 < GSK > +1,0 - bardzo skośny dodatnio
|
|
Spłaszczenie |
C. E. Van Orstrand (1925), W. C. Krumbein (1936) - metoda momentów
|
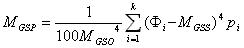
|
gdzie: |
Øi - punkt środkowy i-tego przedziału
klasowego w jednostkach |
pi - częstość i-tego przedziału klasowego
w procentach
k
- liczba przedziałów klasowych
|
MGSS - moment centralny pierwszego
rzędu |
MGSO - moment centralny drugiego rzędu
|
R. L. Folk i W. C. Ward (1957)
|
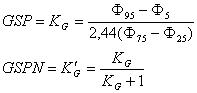
|
gdzie:
|
GSP - spłaszczenie rozkładu uziarnienia |
GSPN - znormalizowane spłaszczenie rozkładu uziarnienia
|
gdy: |
0.41 > GSP > 0,67 natomiast 0,29 > GSPN > 0,40 - rozkład bardzo
platykurtyczny |
0.67 > GSP > 0,90 natomiast 0,40 > GSPN > 0,47 - rozkład platykurtyczny
|
0.90 > GSP > 1,11 natomiast 0,47 > GSPN > 0,53 - rozkład mezokurtyczny |
GSP = 1,00 i GSPN = 0,50 - rozkład normalny
|
1,11 > GSP > 1,50 natomiast 0,53 > GSPN > 0,60 - rozkład leptokurtyczny
|
1,50 > GSP > 3,00 natomiast 0,60 > GSPN > 0,75 - rozkład bardzo
leptokurtyczny
|
| 3,00 > GSP natomiast 0,75 > GSPN > 1,00 - rozkład skrajnie leptokurtyczny
|
| |
| |
| Przeliczanie
jednostek |
| W. C. Krumbein (1934,1964), J. McManus (1963)
|
| - przejście z mm na Ø
|
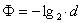 |
| |
| - przejście z Ø na mm |
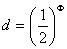 |
| |
| gdzie: |
| Ø - średnica ziaren wyrażona
w jednostkach skal |
|
d - średnica ziaren wyrażona w mm
|
|
